Load LinkageDesigner package
Convert the linage into time dependent linkage
Calculate mass properties of the linkage. Uniform density of 70 kg/m^3 is used
Calculate the generalized forces based on the inverse dynamics of the pendulum
Calculate the substitution values for one complete rotation
Show the calculated torque function of the rotational joint, which is the generalized force of the driving variable
Define the calculated torque as an interpolated function of the

1 driving variable
Copy LinkageData of pend to pend1 variable
Assign the interpolated torque function to act on link1 of the pendulum
Solve the Lagrangian's equation for the pendulum driven by the calculated torque function, for one whole rotation
Plot the time-driving variable function for [0,2
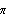
] interval
Animate the movement of the linkage
Calculate the movement of the pendulum if a constant torque is applied.
Solve the Lagrangian's equation for the pendulum driven by the constant torque
Plot the time-driving variable function for [0,2
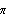
] interval